L’intelligence artificielle est un sujet de plus en plus discuté en société : les technologies grand public sont dotées de plus en plus de compétences, à l’instar de ChatGPT ou d'autres chatbots en vogue depuis fin 2022. Nous parlons d’ailleurs souvent de Machine Learning, ces algorithmes capables “d’apprendre”, et nous les représentons parfois comme des neurones - voire comme un robot de Terminator, mais ceci est un autre sujet.
Image souvent utilisée pour représenter un réseau de neurones artificiels.
Il existe en réalité une multitude d’algorithmes qui permettent à une machine d’apprendre - cette notion sera bien définie dans cet article - et ceux-ci peuvent être très simples ! Nous démystifierons une partie de ce domaine pour mieux appréhender ses évolutions et ses futures conséquences.
Nous allons utiliser un problème désormais ultra-classique pour introduire des concepts mathématiques derrière de nombreux algorithmes modernes : la distance. Il s’agit ici de vulgarisation, aucune connaissance particulière n’est nécessaire : il suffit de quelques souvenirs de géométrie pour se représenter mentalement un espace en trois dimensions.
Le Machine Learning, késako
La plupart des algorithmes informatiques que nous utilisons aujourd’hui ne relèvent pas du Machine Learning ! Il s’agit en réalité de code qui effectue des tâches en se basant sur des règles dictées par le développeur. Ce processus guidé, parfois aléatoire, est donc implémenté en parfaite connaissance de cause.
À l’inverse, un algorithme de Machine Learning va “deviner” tout seul des règles que nous-mêmes ne connaissons parfois pas. Par exemple, sur quels critères peut-on reconnaître informatiquement un objet dans une image ? Nous pourrions créer des algorithmes basés sur les formes, les couleurs… mais une machine dotée d’apprentissage sera plus efficace pour déterminer en autonomie les critères de description d’une image.
Il existe deux grandes familles d’algorithmes d’apprentissage :
- L’apprentissage supervisé : on entraîne la machine avec un jeu de données existant, à partir duquel les règles sont déterminées. Le développeur devra s’assurer qu’elles soient “générales”, et que le modèle n’a pas simplement appris par cœur à quoi ressemblaient nos données. Rentrent dans cette catégorie la reconnaissance d’images ou, plus récemment, les modèles de langage (ChatGPT et autres).
- L’apprentissage non supervisé : l’algorithme n’est pas entraîné, il ne connaît donc pas les règles à l’avance. Cela permet, par exemple, de regrouper ensemble des objets en fonction de leur ressemblance selon différents critères, donnant davantage de flexibilité à l’algorithme que si l’humain apportait ses propres catégories.
Le Machine Learning possède de nombreuses applications :
- la régression : trouver une valeur numérique, comme le prix d'un bien immobilier,
- la classification : attribuer une classe, comme la nature d'un objet dans une image,
- le clustering : créer des groupes d'éléments similaires sans titre particulier.
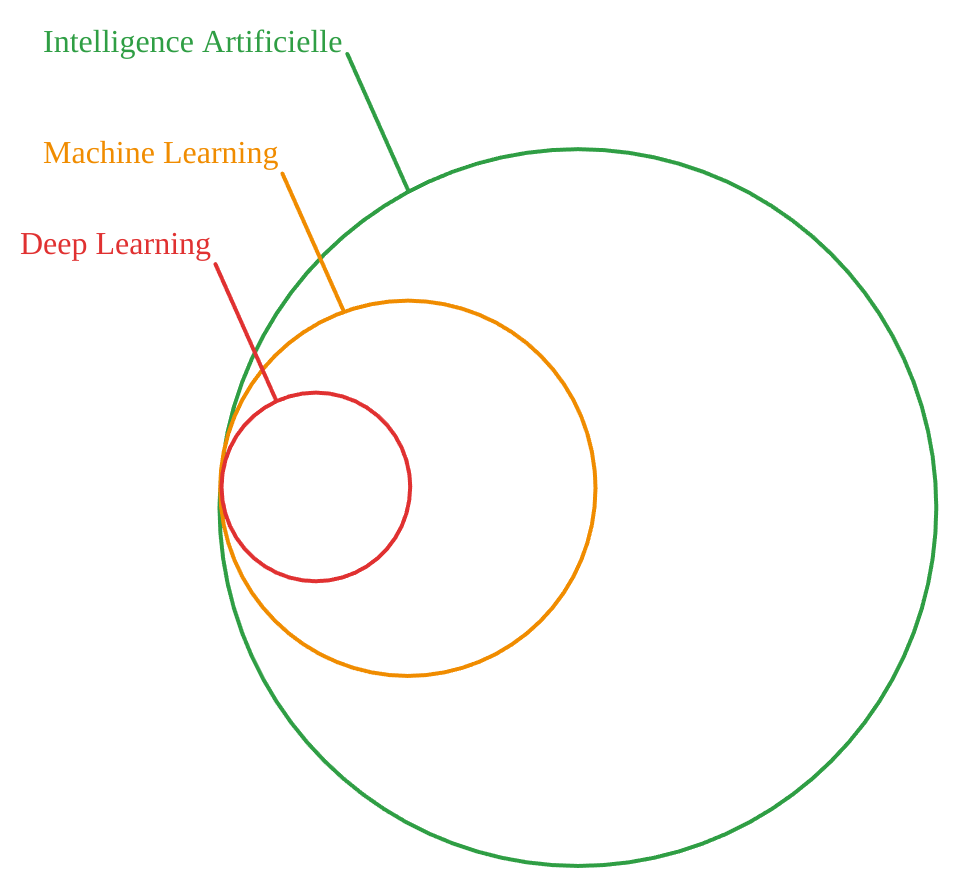
Enfin, le Deep Learning est une typologie d'algorithmes d'apprentissage supervisé, utilisant la minimisation d'une fonction objectif : les réseaux de neurones en sont un exemple classique. Nous introduirons plus en détail cette notion dans un prochain article, en donnant comme exemple la prédiction de la difficulté d’une voie d’escalade.
Pour résumer, le domaine de l’Intelligence Artificielle est vaste, et il convient de bien séparer les concepts en jeu !
Présentation du problème et approche naïve
Le problème est le suivant : présenter une image contenant un chiffre arabe manuscrit à un ordinateur, et lui demander quel est ce nombre. Un problème plus large vise à reconnaître des caractères, voire des textes manuscrits, mais nous nous limiterons ici à la reconnaissance de chiffres. Nous nous appuierons pour cela sur la base de données MNIST.

Exemple d’images issues de la base de données MNIST
La méthode courante serait de directement implémenter un modèle de reconnaissance d’images, basé sur des réseaux de neurones pouvant tout faire, mais plusieurs considérations apparaissent.
- Notre problème est relativement simple : reconnaître des chiffres, soit 0,00…01 % des cas d’usage réel. Utiliser un modèle lourd simplement pour cette tâche entraînerait d’importants coûts en calcul informatique, donc en énergie électrique, et donc en argent.
- Entraîner un modèle très performant avec “peu” de données (ici seulement des chiffres) peut avoir de moins bons résultats, car le processus d’apprentissage pour un réseau de neurones contient une part d’aléatoire.
Ce modèle complet de reconnaissance d’images n’est cependant pas à abandonner définitivement ! Il pourrait également parfaitement résoudre le problème, mais l’objectif de cet article est simplement de vulgariser un des algorithmes d'apprentissage et d’introduire des concepts mathématiques fondamentaux.
Une affaire de distance...
Faisons un détour par le monde de la géométrie, le lien avec notre problème initial apparaîtra naturellement. Vous connaissez déjà le concept de dimensions : 1D, 2D, 3D, voire 4D et plus. Nous pouvons les représenter respectivement par une droite, un plan et un espace ; pour les dimensions supérieures, il faut malheureusement faire appel à l'intuition ou à des représentations simplifiées.
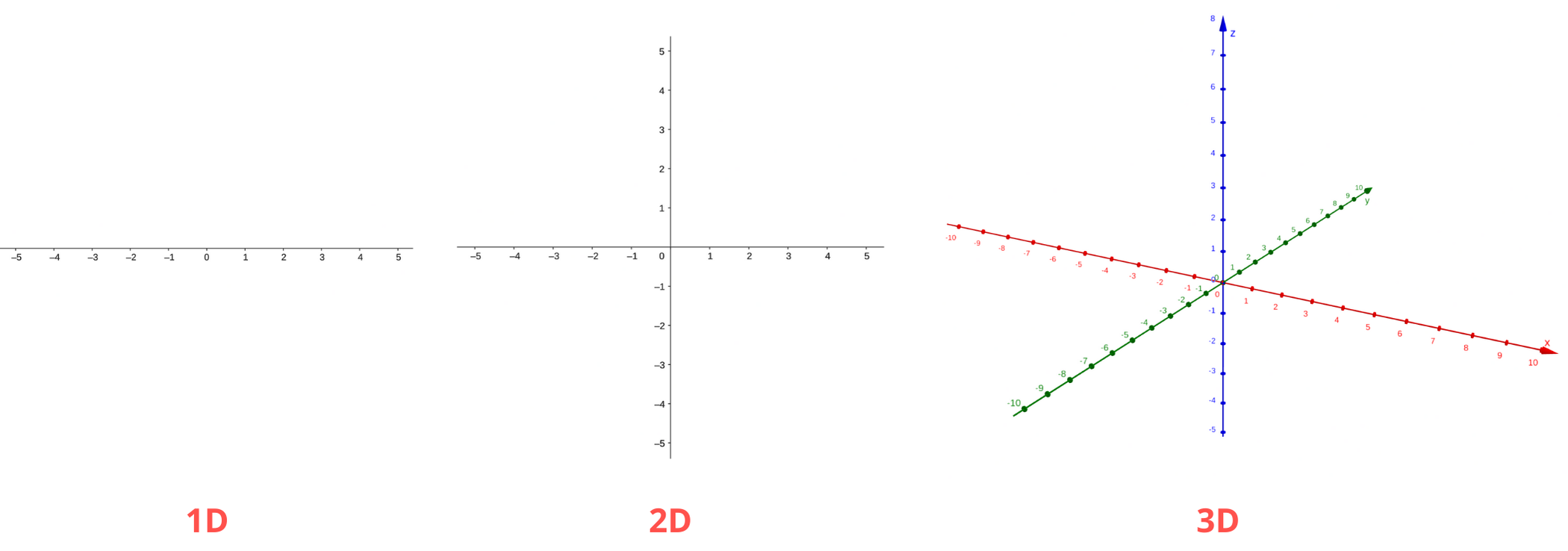
Ajout progressif de dimensions à un espace, matérialisées par des axes gradués.
Dans ces espaces sont placés des points, représentés par des coordonnées : par exemple, en trois dimensions, un point aura trois nombres comme coordonnées. Supposons que dans ce même espace 3D se situent de nombreux points que l'on peut distinctement séparer en plusieurs groupes, appelés classes. Si nous plaçons un nouveau point qui n'est a priori classé dans aucun de ces groupes, comment choisir au mieux son appartenance ? Il est ici demandé une solution rationnelle, sans faire appel à notre intuition humaine mais seulement à un algorithme qui ne connait que les coordonnées, donc un ensemble de nombres !
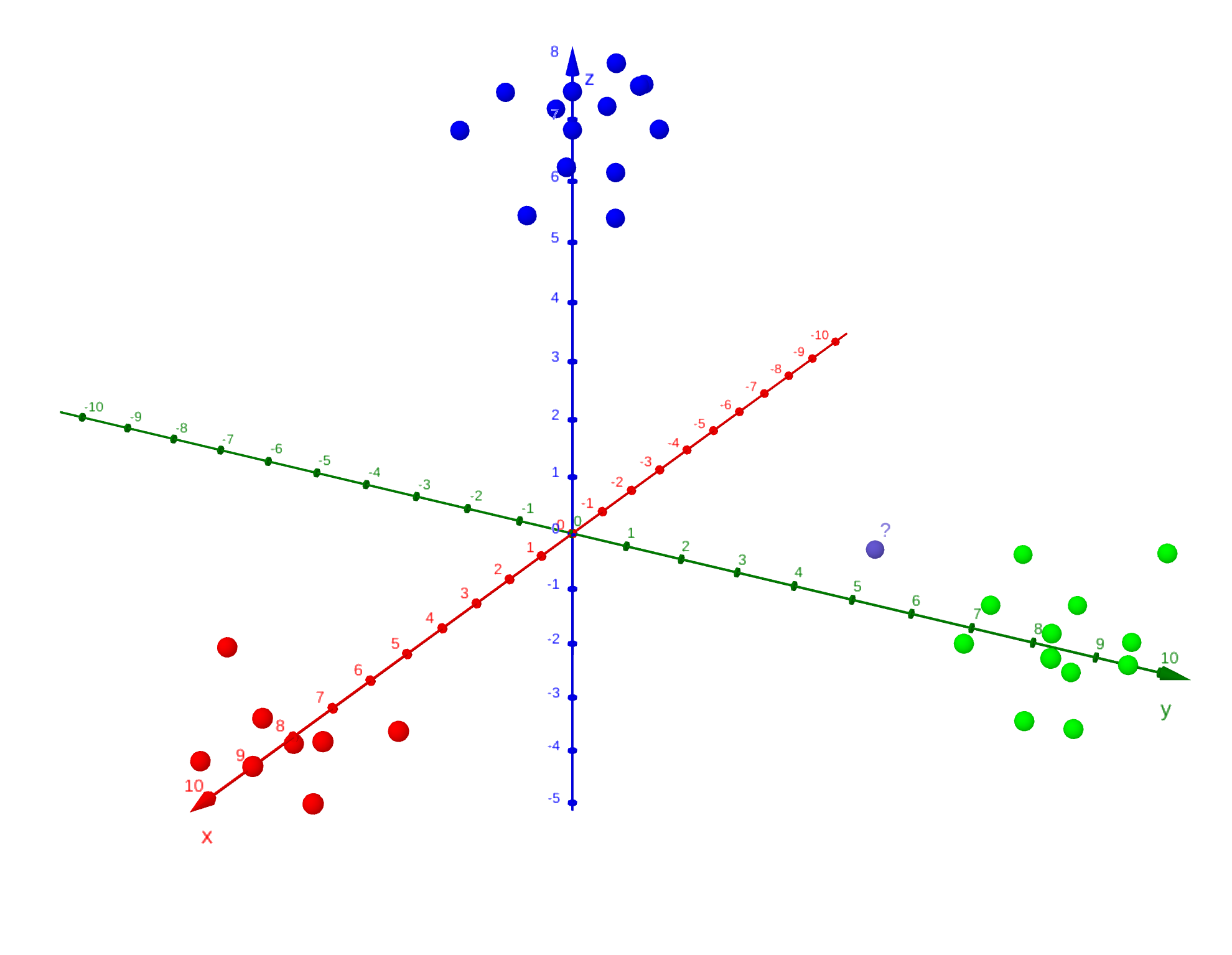
Un espace avec trois groupes de points : rouge, vert et bleu. À quel groupe appartient le point violet ?
Il est possible de faire appel à la notion de distance entre les points : comme il est impossible d’utiliser une règle graduée en informatique, l’algorithme tirera directement parti des coordonnées. La formule peut être vue comme une généralisation à trois dimensions du théorème de Pythagore :
avec les deux points entre lesquels calculer notre distance. Ainsi, l’algorithme considère un certain nombre de voisins, disons , et définit alors la classe du nouveau point comme la classe majoritairement présente parmi ses voisins. Il s'agit alors de l'algorithme des k plus proches voisins.
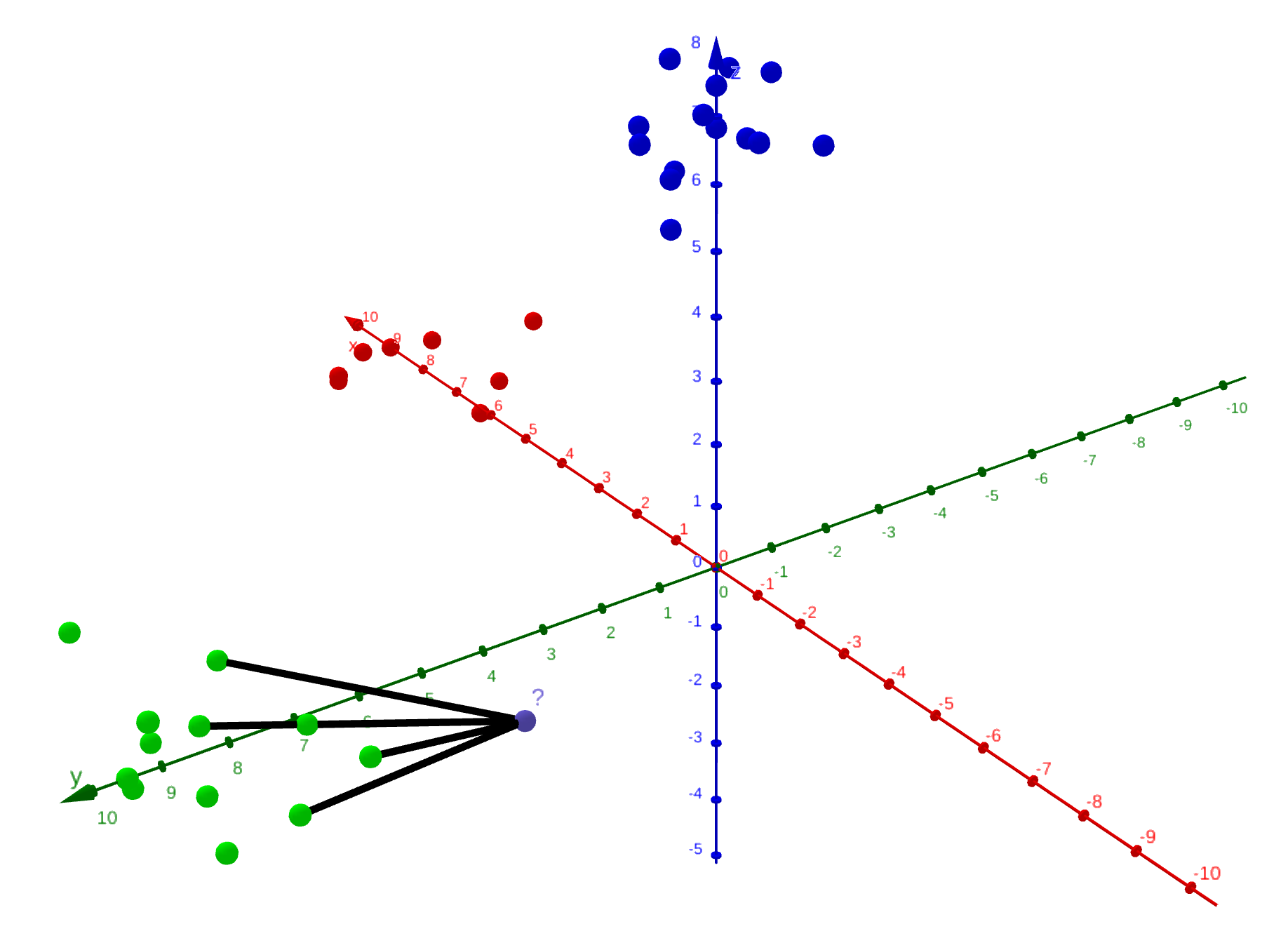
Le groupe du nouveau point est déterminé grâce à celui de ses 5 plus proches voisins : ici, le point appartient au groupe vert.
Dans un premier temps, nous allons appliquer ce principe à de petites images de taille 3x1 en échelle de gris, pour ensuite généraliser et résoudre notre problème initial.
Ces images sont donc représentées dans notre espace par leurs 3 coordonnées comprises entre 0 (noir) et 255 (blanc), et peuvent être séparées en trois classes : celles dont le premier pixel est le plus clair, et ainsi de suite pour les deux autres pixels.

Les classes d’images que nous utiliserons pour expliquer comment résoudre le problème de la reconnaissance de chiffres.
Pour déterminer la classe d’une image jamais étudiée jusqu’à présent, il suffit de déterminer celle de ses plus proches voisins.
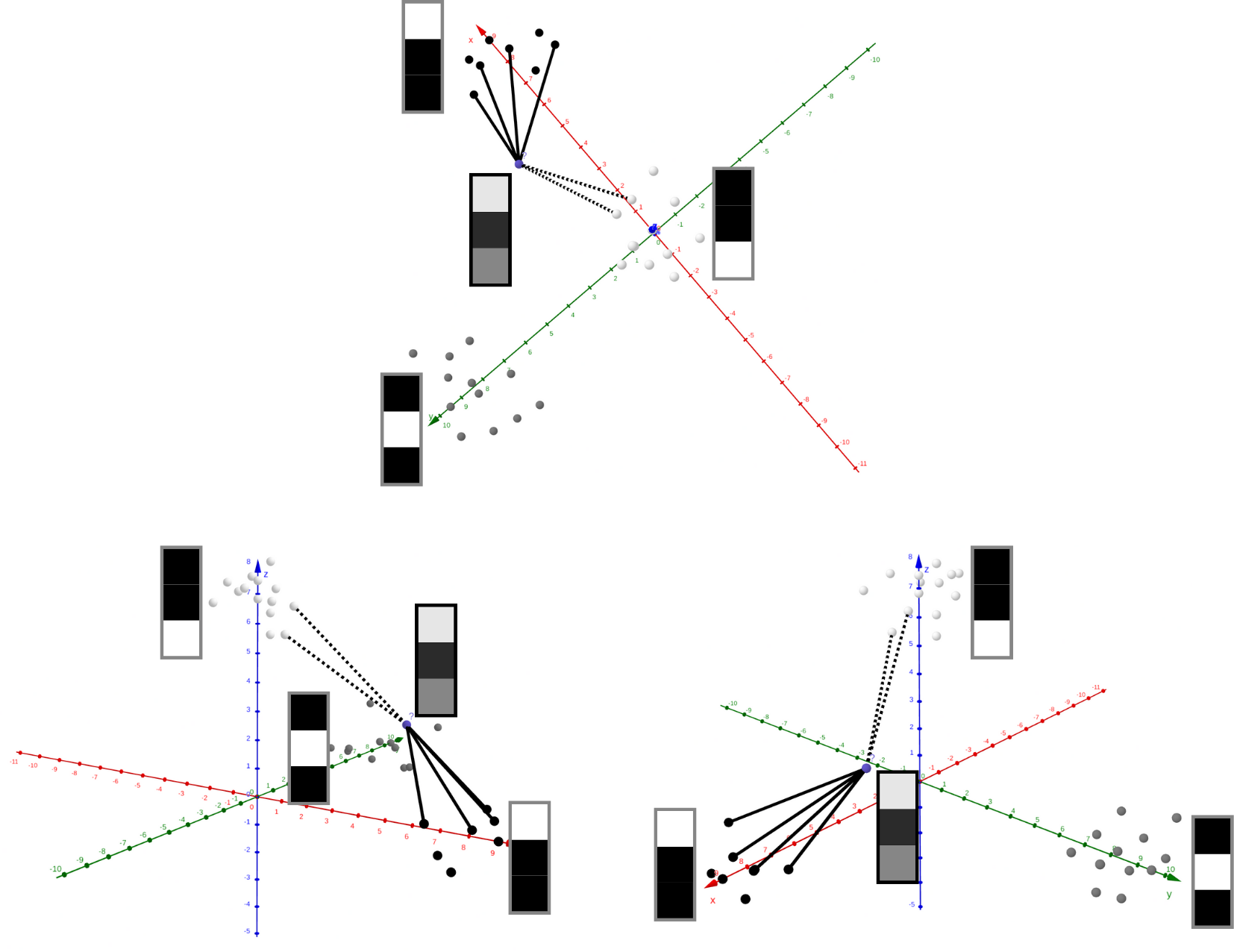
Vues sous trois angles différents de l’exécution de notre algorithme, avec k=6 voisins.
Ici, la majorité d’entre eux appartiennent à la classe “pixel du haut”, notre image est donc classifiée ainsi.
Nous pouvons à présent résoudre le problème initial de la reconnaissance de chiffres.
Appliquons ce principe aux chiffres
Nos images sont ici légèrement plus compliquées : elles sont certes en échelle de gris, mais sont de taille 28 par 28. Nous les placerons donc dans un espace comportant dimensions : nous ne pouvons plus le visualiser en entier, mais le principe des coordonnées reste le même. Par la suite, nous représenterons cet espace en trois dimensions pour mieux visualiser les résultats.
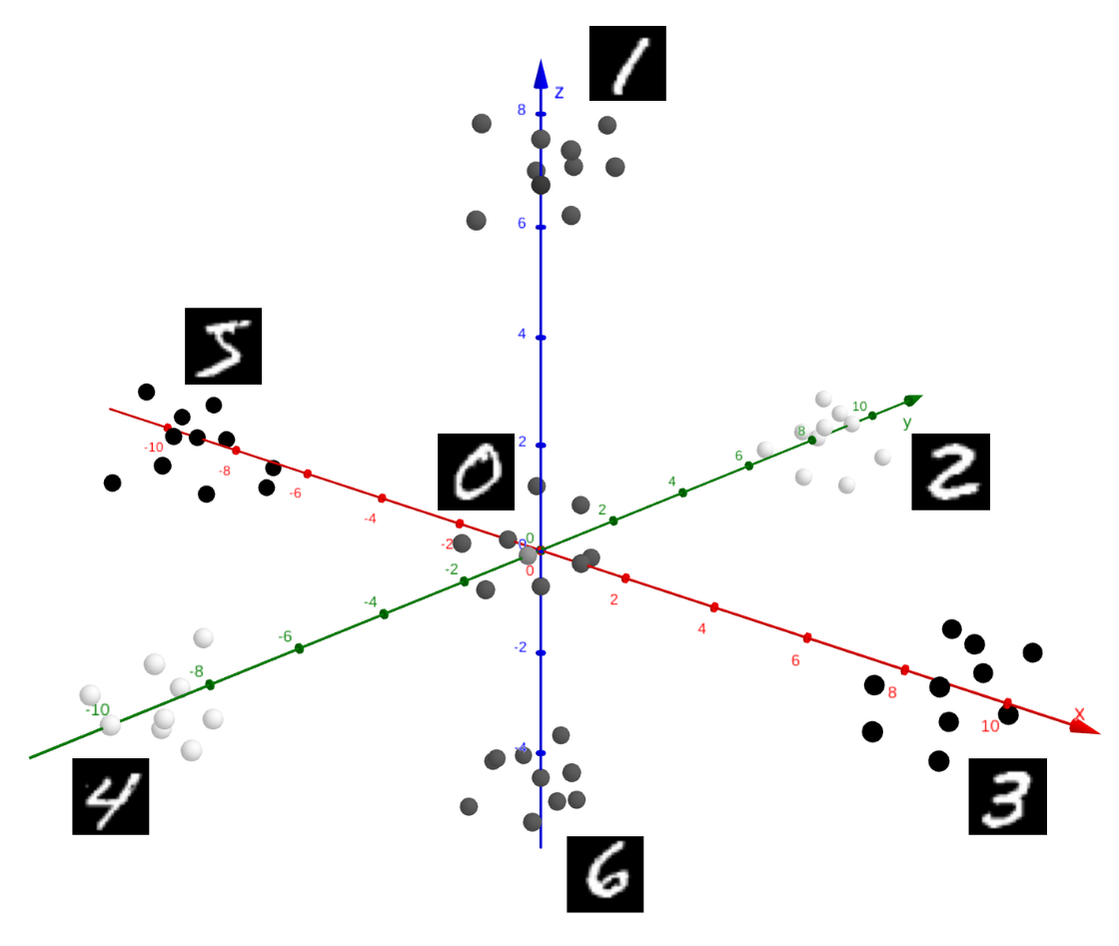
Représentation schématique de l’espace dans lequel sont placés nos images de chiffres manuscrits.
Traitons alors ces images comme des points et appliquons l'algorithme des plus proches voisins. Le tableau suivant, appelé matrice de confusion, résume les résultats de l'algorithme :
- la ligne indique le chiffre contenu réellement dans l'image,
- la colonne indique la prédiction effectuée par le modèle,
- le chiffre de la case indique alors le pourcentage d’images affichant un chiffre , qui ont été classées comme “chiffre ”.
L’algorithme est d’autant plus efficace que les pourcentages se concentrent sur la diagonale, c’est-à-dire que le modèle a bien prédit le chiffre pour une image comportant le chiffre .
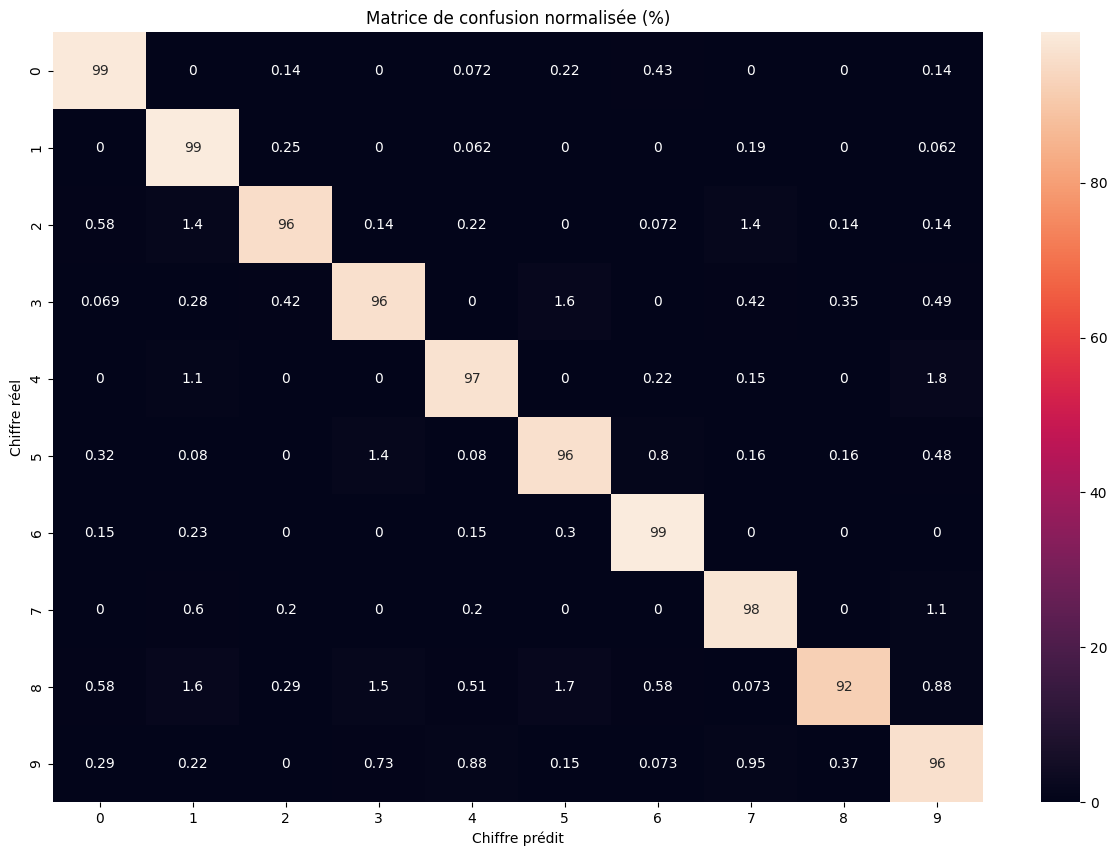
Matrice de confusion obtenue après évaluation de notre modèle
| Chiffre | Exactitude (%) |
|---|---|
| 0 | 99 |
| 1 | 99 |
| 2 | 96 |
| 3 | 96 |
| 4 | 97 |
| 5 | 96 |
| 6 | 99 |
| 7 | 98 |
| 8 | 92 |
| 9 | 96 |
Tableau récapitulatif de l'exactitude de notre modèle en fonction du chiffre à prédire
L'algorithme est très performant, avec une exactitude moyenne de 97%, et ce pour un temps de calcul de 27 secondes en comptant les phases d’entrainement et de prédiction. Plusieurs avantages apparaissent en comparaison à la reconnaissance d'images générale.
- Il est peu coûteux en optimisant la structure. Par coût, nous entendons "temps d'exécution" pour réaliser une prédiction, or le temps c'est de l'argent. À la fin de l'article, je donne dans une partie bonus une des clés pour optimiser cet algorithme.
- L'explicabilité est maximale. Nous pouvons parfaitement expliquer les prédictions de ce modèle, simplement en affichant les images les plus proches et la classe majoritaire. L'explicabilité est un sujet important en intelligence artificielle, surtout à l'aube de réglementations exigeantes, comme l'AI Act en Europe.
La distance, un principe qui perdure
Pour cette typologie de problèmes, nous utilisons plutôt des gros modèles, car ils ont le mérite de se généraliser à toutes les images et d’apprendre de leur complexité. Cependant, les notions mathématiques d’espace et de distance sur lesquelles se base l’algorithme des plus proches voisins perdure. Nous allons survoler deux exemples s’en rapprochant, vous pouvez les approfondir si vous le souhaitez.
Collaborative Filtering
Cet algorithme vise à recommander des “objets” au sens large à des utilisateurs en se basant sur des similarités entre les comportements. Nous pouvons citer par exemple la recommandation d’un film sur une plateforme de streaming.
Pour cela, l’algorithme construit un tableau dont les lignes représentent les différents utilisateurs, et les colonnes représentent les objets. On coche la case dès que l’utilisateur a “interagit” avec l’objet : par exemple, s’il a regardé le film sur Netflix, ou acheté le produit sur Amazon. Chaque ligne et chaque colonne peut alors être interprétée comme un ensemble de coordonnées représentant un point : il suffit de calculer une moyenne sur les k plus proches voisins pour déterminer le comportement de l’utilisateur et lui suggérer de nouveaux objets !

Tableau fictif représentant les achats de différents utilisateurs sur une boutique en ligne
Pour aller plus loin : Article d’IBM (en anglais)
Embedding pour le traitement du langage naturel (NLP)
Nous alors survoler ici une notion essentielle aux modèles qui traitent le langage naturel de manière avancée, comme ChatGPT. Un tel algorithme n’a pas de raison en soi de considérer qu’un mot donné a du “sens”, et encore moins une phrase entière avec du contexte. La sémantique est une notion humaine complexe car elle fait appel à des représentations mentales abstraites.
Nous allons alors utiliser la force des espaces multi-dimensionnels - douze-mille dimensions environs pour GPT 2 - et représenter chaque mot* par un point. Deux mots proches au sens de la distance sont alors proches sémantiquement : par exemple, “roi” est proche de “royaume” et de “couronne”, etc…
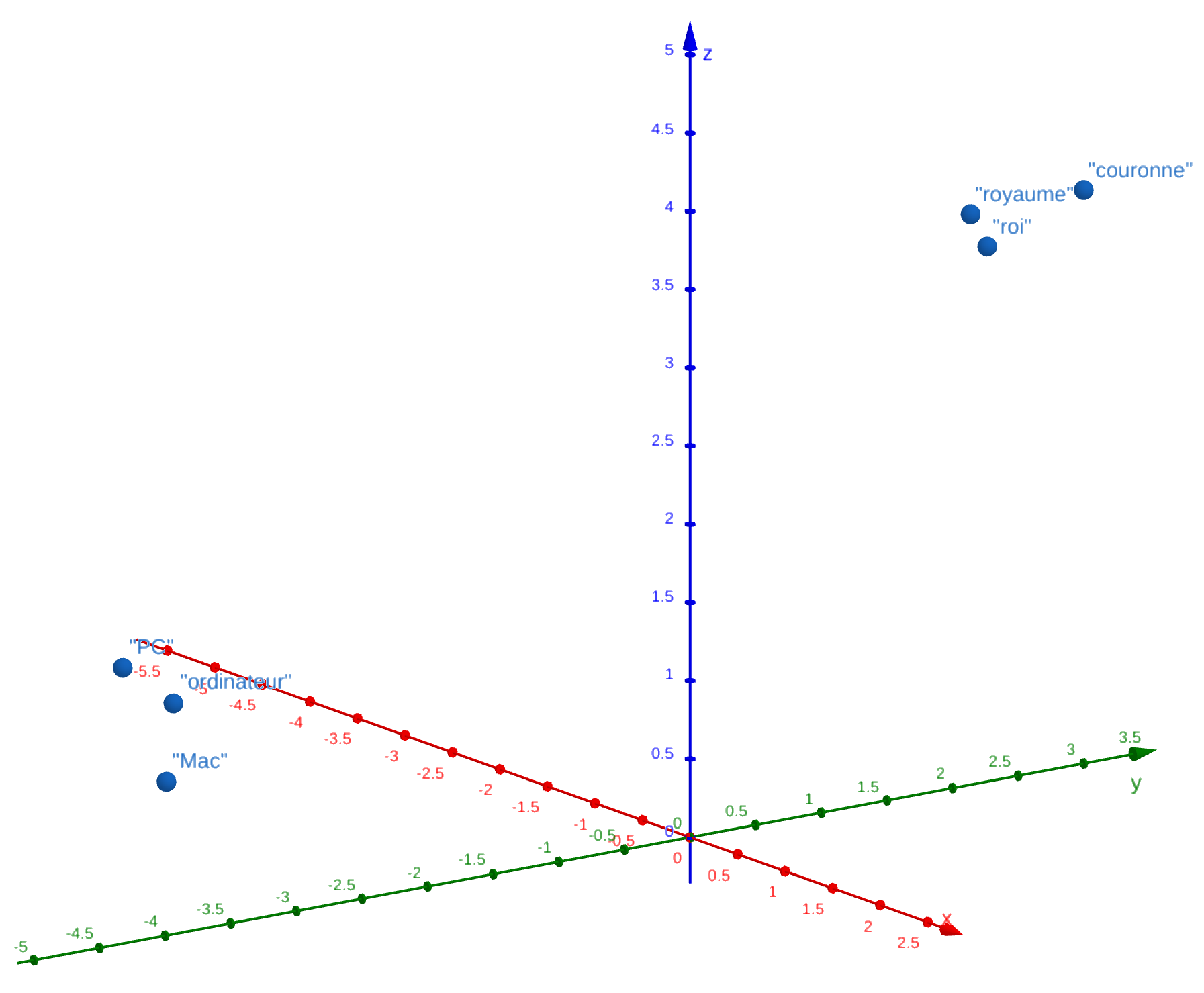
Représentation schématique de l’espace où sont situés les mots. Plus ils sont proches au sens de la distance, plus leur sens se ressemble.
Un ensemble de mots, tel une phrase ou un début de phrase, représente alors une trajectoire dans cet espace : pour déterminer le mot suivant, l’algorithme observe les plus proches voisins du point final de la trajectoire. C’est pourquoi ChatGPT génère une réponse mot après mot : pour chaque morceau de phrase en cours de construction, son algorithme détermine dans cet espace le mot qui doit suivre. La structure sous-jacente est évidemment bien plus complexe et des modules neuronaux permettent de contextualiser et donner du sens aux mots.
* En réalité, l’algorithme ne traite pas des mots mais des “tokens”, des ensembles de lettres.
Pour aller plus loin : Vidéo de 3blue1brown
Conclusion
À travers cet article, nous avons exploré les principes mathématiques d’espace et de distance qui forment la structure de nombreux algorithmes : certains problèmes peuvent alors être résolus de manière efficace sans sortir l’arme lourde !
La branche mathématique complète, l’algèbre linéaire, est omniprésente dans nos ordinateurs - même pour afficher des objets en 3D à l’écran - à tel point que les cartes graphiques sont optimisées pour réaliser ces opérations le plus efficacement possible.
Si vous souhaitez en apprendre davantage sur le Machine Learning voire coder vos propres algorithmes, vous pouvez jeter un oeil à ma page Notion qui regroupe de nombreuses ressources en la matière. Vous pouvez également me contacter pour prolonger la discussion.
Bonus : dans la pratique
Avec scikit-learn
Nous pouvons tirer parti de la librairie scikit-learn en Python, très populaire auprès des data sicentists. Nous utilisons également des utilitaires pour afficher les données montrées dans cet article.
from sklearn.datasets import fetch_openml
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
import numpy as np
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
# Chargement du jeu de données MNIST
X, y = fetch_openml("mnist_784", version=1, return_X_y=True, as_frame=False)
# Affichage de quelques images pour prendre connaissance des données
fig, axs = plt.subplots(nrows=10, ncols=10, figsize=(10, 10))
for i in range(100):
plt.sca(axs[i // 10, i % 10])
axs[i // 10, i % 10].axis('off')
plt.imshow(X[i].reshape(28, 28), cmap='gray', vmin=0, vmax=255)
fig.tight_layout()
# Séparations des données en deux jeux :
# - une partie constitue le "jeu d'entrainement", c'est-à-dire les images classifiées et placées à l'avance dans l'espace,
# - une autre partie constitue le "jeu de test", dont les catégories seront prédites par notre modèle, ce qui permet de l'évaluer.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# Entrainement du modèle
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
# Évaluation du modèle : exactitude moyenne
y_pred = knn.predict(X_test)
print(f'Exactitude moyenne : {knn.score(X_test, y_test)}')
# Évaluation du modèle : matrice de confusion
cm = confusion_matrix(y_test, y_pred)
# Normalisation de cette matrice : les cases contiennent des effectifs, qu'on convertit en pourcentages
cm_normalized = cm.astype('float') * 100 / cm.sum(axis=1)[:, np.newaxis]
plt.figure(figsize=(15, 10))
sns.heatmap(cm_normalized, annot=True, cmap='rocket')
plt.xlabel("Chiffre prédit")
plt.ylabel("Chiffre réel")
plt.title("Matrice de confusion normalisée (%)")
# Évaluation du modèle : exactitude par classe
per_class_accuracy = cm.diagonal() / cm.sum(axis=1)
pd.DataFrame([[i, acc * 100] for i, acc in enumerate(per_class_accuracy)], columns=['Chiffre', 'Exactitude (%)'])
# Affichage des graphiques
plt.show()
À la main, avec une structure optimisée
Notre algorithme se base sur la distance entre des points, ce qui n’est pas naturellement une méthode efficace. Un programme informatique ne peut pas “voir” les points : sans optimisation, il doit calculer la distance d’un point avec tous les autres points pour déterminer ses voisins ! Heureusement, des structures efficaces existent, comme les arbres k-dimensionnels.
Cette structure garde en mémoire les points sous forme d’un arbre, que l’on peut visualiser comme un organigramme. Chaque partie de l’espace est récursivement découpée en deux morceaux selon une des dimensions : pour le parcourir, il suffit alors de regarder successivement les valeurs des coordonnées du point étudié. Cette structure nous permet de trouver des voisins beaucoup plus efficacement.
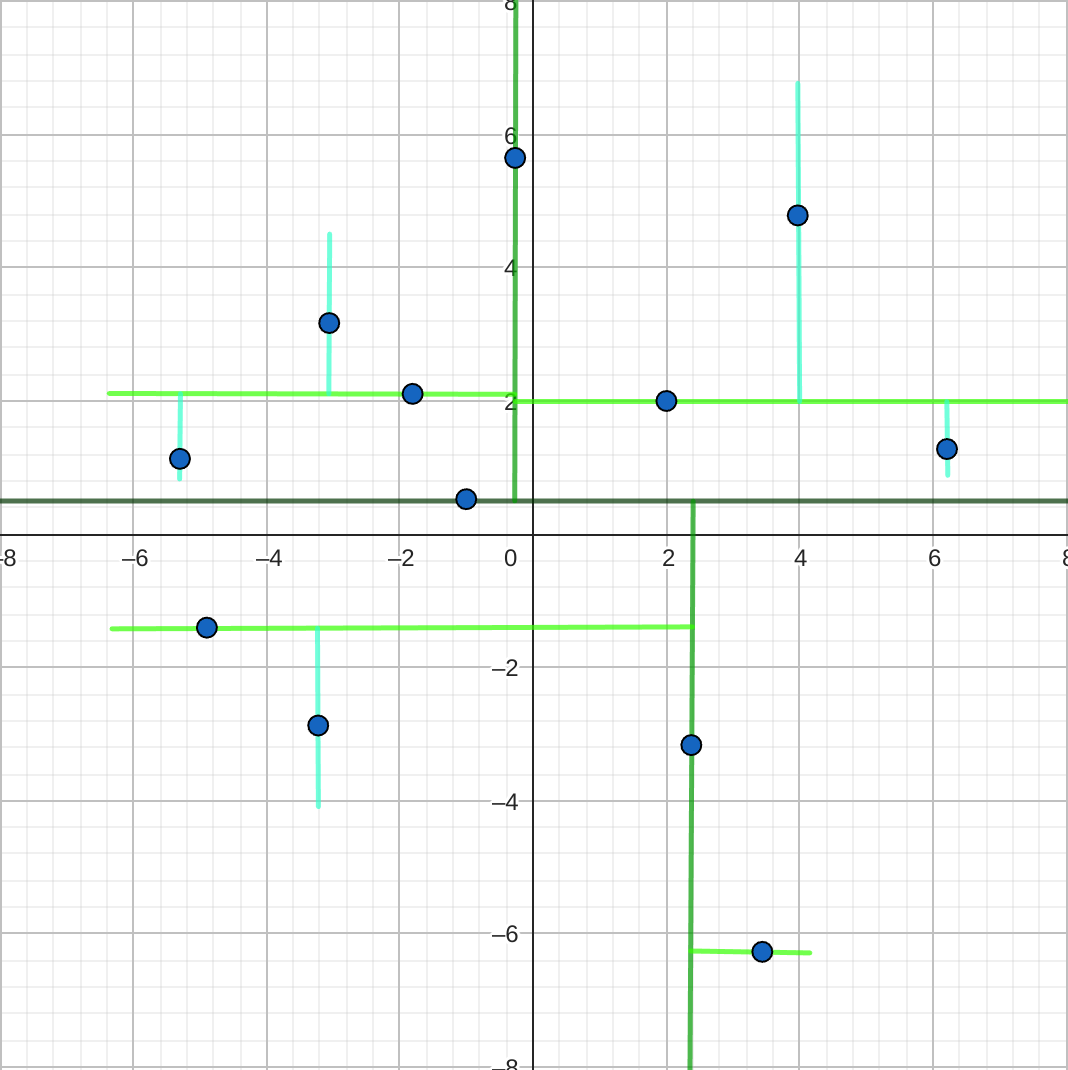
Schématisation d'une arbre k-dimensionnel, en deux dimensions
Dans le cadre de ma classe préparatoire informatique, j’ai implémenté l’algorithme des k plus proches voisins avec la structure d’arbre k-dimensionnel. Le code complet est disponible sur GitHub, en langages C ou OCaml.
Partager la publication
X (Twitter) Facebook Diaspora Mastodon MailPublié dans
Article Apprentissage Apprentissage KNN ImagesCatégories
Software Sécurité Web Hardware Programmation Android Linux Windows Apprentissage AppleNos réseaux sociaux
Nous postons régulièrement des nouvelles, des tips et des astuces. Suivez-nous!
Les liens BecauseOfProg
Nous partageons des liens vers des ressources, des blogs ou des publications intéressants, afin que vous puissiez vous aussi les découvrir.
Nos dernières publications
Installer Microsoft Teams 2.0 (New) sur Linux et macOS
Découvrez comment installer la nouvelle version de Microsoft Teams